Laptop Murah Dan Praktis Untuk Mengerjakan Tugas Kuliah Online menjadi kebutuhan penting bagi mahasiswa di […]
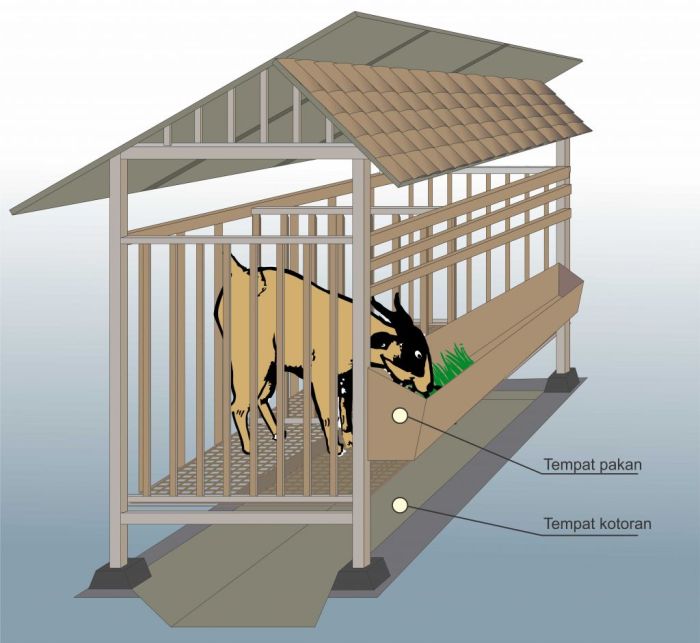
Pembuatan Kandang Ternak Kambing Yang Nyaman Dan Hemat Biaya
Pembuatan Kandang Ternak Kambing Yang Nyaman Dan Hemat Biaya? It’s a total game-changer, dude! Bayangkan, […]
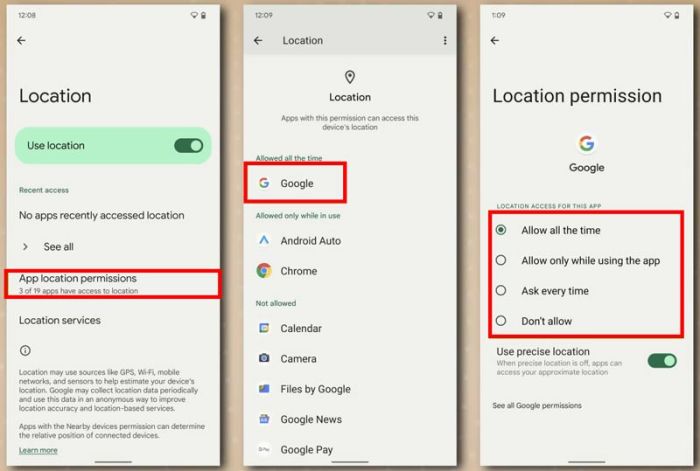
Mengelola Pengaturan Lokasi Di Android
Mengelola Pengaturan Lokasi Di Android: Kuasai perangkat Anda dan lindungi privasi Anda! Pernahkah Anda bertanya-tanya […]
Penggunaan Teknologi Pengolahan Air Limbah Peternakan
Penggunaan Teknologi Pengolahan Air Limbah Peternakan menjadi sorotan seiring meningkatnya kesadaran akan dampak lingkungan. Limbah […]
Penggunaan Teknologi Pengolahan Limbah Ternak Yang Ramah Lingkungan
Penggunaan Teknologi Pengolahan Limbah Ternak Yang Ramah Lingkungan menjadi sorotan utama dalam wawancara eksklusif ini. […]
Laptop Murah Dan Bergaransi Resmi Selama 2 Tahun
Laptop Murah Dan Bergaransi Resmi Selama 2 Tahun menjadi solusi ideal bagi Anda yang menginginkan […]
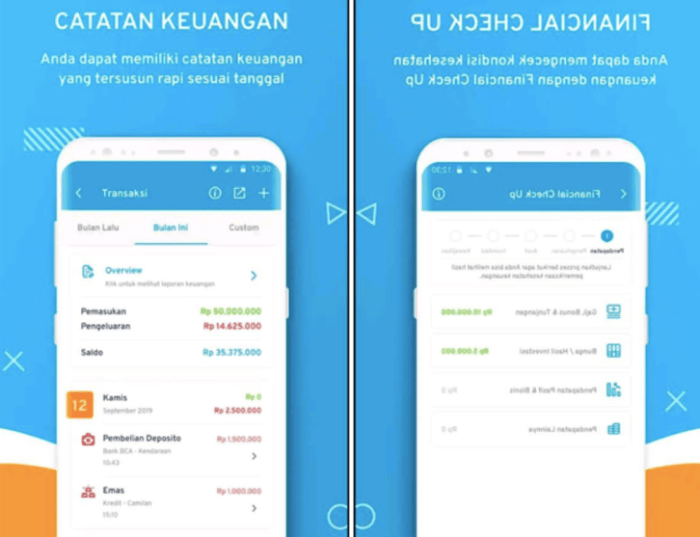
Aplikasi Pencatat Pengeluaran Dan Menabung Yang Mudah Digunakan
Aplikasi Pencatat Pengeluaran Dan Menabung Yang Mudah Digunakan? Udah nggak zamannya lagi deh pusing mikirin […]
Perencanaan Bisnis Budidaya Lobster Air Laut
Perencanaan Bisnis Budidaya Lobster Air Laut: Mimpi untuk meraih kesuksesan di dunia bisnis perikanan, khususnya […]
Mengaktifkan Dan Menggunakan Fitur Face Unlock Di Android
Mengaktifkan Dan Menggunakan Fitur Face Unlock Di Android, eh, kayak buka pintu pake muka aja […]
Laptop Murah Dan Hemat Energi Untuk Penggunaan Baterai Yang Lama
Laptop Murah Dan Hemat Energi Untuk Penggunaan Baterai Yang Lama. Bayangkan, sebuah perangkat yang mampu […]